The maximum principal stress failure forecaster (MPSFP) design rule (Samuel and Weir 1999) stipulates that when an element made of brittle materials is subject to the stress of a multiaxial system. It will fracture when the principal stress anywhere within the component is greater than the strength of the local area.
Stresses on the primary planes are known as principal stresses. The major principal plane carries the greatest amount of normal stress, and the stress that acts on it is referred to as major.
Primary Tension
To summarize, If brittle material is subject to multiaxial stress, the fracture will occur whenever the maximum primary stress exceeds the local strength, according to the MPSFP design rule (Samuel and Weir, 1999).
One, two, and three are the traditional designations for the three major stresses.
When it comes to major stresses, there are the following three levels of stress:
- The highest (tensile),
- Intermediate,
- The lowest (compressive).
Plates, 2D, and volumetric elements may all depict the primary stress (bricks). Tension is indicated by (+) while compression is indicated by (-). An excellent depiction of this may be seen in Mohr’s Circle.
Main Stress And Maximum Shear Stress
The main stress and maximum shear stress calculator designing to calculate principal stresses, maximum shear stresses, stress angles, and Von Mises stress at a given location for plane stress (σz=τzx=τzy=0).
If you want to know the maximum principal stress, you may use ANSYS’s Maximum Principal Stress findings, which are the same as the principal stress.
The maximum normal-stress hypothesis may apply to brittle fractures under tension since the normal tensile stress alone is responsible for the fracture. Normal compressive stress and shear stress must take into account when determining the cause of brittle fracture in compression.
Stresses and strains are inevitable when a body, component, or substance expose to an external load, as we know all too well.
Within the elastic limit, stress is inversely proportional to strain according to Hook’s law; in other words, the shape and size of the thing will change if an external force exerts it. External forces may remove from the body without affecting the body’s structure.
After removing the stress, no lasting deformation will occur in the body if it stays within its elastic limit.
Also check: The Truth About Stress Lines In Teeth: How To Avoid Them?
In cases when the external load exceeds the elastic limit, the body will deform permanently. It means that the distortion will persist even after the force removes. If there is permanent deformation in the body as a result of externally impose load, the component, material, or body is said to have failed.
Using theories of failure, we can figure out a machine component’s safe size and dimensions. When it exposes to the cumulative stresses that result from the numerous loads operating on it while it is in operation.
There are a number of hypotheses that might explain why a component or body fails when exposed to external stresses.
- The notion of maximal primary stress
- The hypothesis of maximal primary strain and maximal shear stress
- The maximum strain energy hypothesis
- The theory of maximum shear stress and energy
- The notion of maximal primary stress is the first thing we will cover.
- In accordance with the notion of maximum primary stress, failure occurs when the greatest value of principal stress generated in the body reaches the limiting value of stress.
- In order to fail, the body can only take so much stress.
- To ensure the safety of a product,
- Stressors that can tolerate in the body less the maximum amount of stress that can create in the body.
Acceptable Stress
The simplest definition of acceptable stress is the ratio of failure stress, i.e., ultimate stress or yield stress, to the safety factor.
F.O.S. = allowable stress in terms of ultimate stress, yield stress, and other related concepts.
There are a number of important aspects to the notion of maximum primary stress, It is also known as Rankine’s theory because of its emphasis on maximum primary stress.
When designing a machine component comprised of brittle material, the maximum main stress hypothesis makes sense since brittle materials are weak under tension. If composed of ductile materials, the maximum primary stress theory is not appropriate since shear failure might occur.
Maximum Primary Stress Theory
Designing ductile-material machine components may benefit from using the maximum primary stress theory under the following three conditions.
- Tension in a single direction
- Stress in a biaxial condition when the major stresses are of the same kind.
- Hydrostatic pressure exerts
Normal Stress
As its name indicates, normal stress occurs when the deforming force applies perpendicular to the body’s cross-sectional area. When the wire’s length or body volume fluctuates, the stress level will be normal.
Polynomial equations of the second degree use to express the effects of stress on a body in multiple planes of motion.
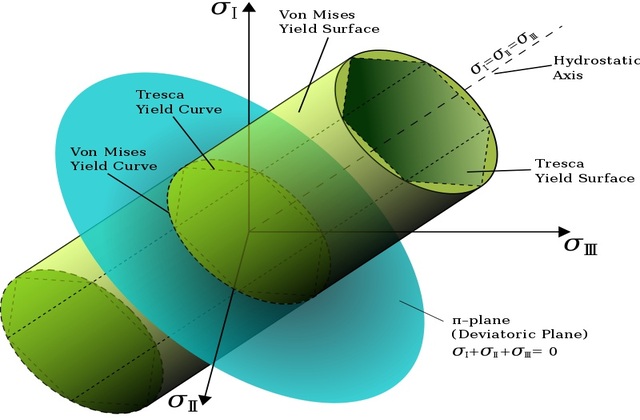
Von Mises Stresses
It is possible to tell whether a material will yield or fracture based on its Von Mises stress. Metals and other ductile materials are good candidates for this process.
Using the von Mises criteria, we can simply compare the allowed tension to the tensile stress in the material.
It is possible to calculate von Mises stress by measuring the forces operating on any given structure. This enables us to determine the yielding (or failure) of a ductile material. When the basis of another stress tensor is zero, the components of stresses says to be principal stresses.
The von Mises Stress Calculator
- It is easy to see that V is equal to the product of the square root of two and the square root of three times three.
- Direction X of stress.
- Y Direction – Y Stress.
- XY Shear Stress.
A second-degree polynomial equation may use to depict the strain on a body in several directions.
